电信类专业的一门重要课程是随机过程,这门课的概率论以实变函数、测度论为基础,而学习测度论的过程中无可避免地会遇到一些抽象代数的概念,本文对相关概念进行简单总结

终极总结: 群是一些有基本对称性的东西,域是一些像实数复数的东西,环是一些像多项式、矩阵的东西
群
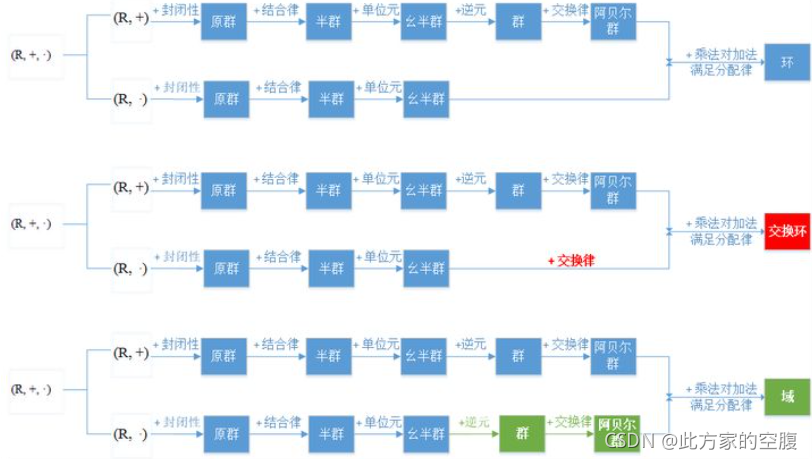
在数学中,群(group)是由一种集合以及一个二元运算所组成的代数结构,并且符合“群公理”。群公理包含下述四个性质,分别是封闭性、结合律、单位元和对于集合中所有元素存在逆元素。群是一些有对称性的东西
定义
群\((G,\cdot)\)是由集合G和二元运算"·"构成的,\(\cdot为二元运算: M \times M \rightarrow M\)。符合以下四个性质(称“群公理”)的数学结构。其中,二元运算结合任何两个元素a和b而形成另一个元素,记为a·b,符号"·"是具体的运算,比如整数加法。
四个群公理为:
- 封闭性。\(a\cdot b\)仍然在集合G中
- 结合律。\((a \cdot b)\cdot c= a \cdot (b \cdot c)\)
- 单位元。存在G中的一个元素e,使得对于所有G中的元素a,总有等式e·a = a·e = a 成立。
- 逆元。对于每个G中的a,存在G中的一个元素b使得总有a·b = b·a = e,此处e为单位元。
\(Remark:\)
- 封闭性非常自然,不用多讨论。2、3、4三点结合起来保证群有一种很基本的对称性。例如整数加法群,群公理2要求(a+b)+c=a+(b+c)(运算次序对结果无影响,是代数结构的基本对称性),群公理三要求有单位元数字0(对称的中心点),群公理4保证了这个整数群正负对称
- 群的四公理不要求二元运算有交换性。如果这个二元运算还有交换性,即a*b=b*a,称这个群为交换群(或Abel群),这个群有更强的对称性;否则称为非交换群
- 群四公理是有顺序的。仅满足1为原群,再加上2为半群,再加上3为幺半群(幺的意思就是1,含有单位元),再加上4称为群。如果还加上交换性,也就是阿贝尔群
域
域是一些像实数复数以及定义在上面的像加法、乘法的东西。更严格来说,有如下规定
域由集合F以及定义在上面的两种二元运算代数结构构成,即\((F,+,*)\),它满足如下八条公理(线性空间也是八条公理,这八个公理很像)。对 \(\forall a, b, c \in F\)
- 对加法和乘法都封闭
- 加法和乘法都分别符合结合律
\(\forall a, b, c \in F,(a+b)+c=a+(b+c),(a * b) * c=a *(b * c)\)
- 加法和乘法都分别符合交换律
\(\forall a, b \in F, a+b=b+a, a * b=b * a\)
- 乘法对加法有分配律
\(\forall a, b \in F, a+b=b+a, a * b=b * a\)
- 存在加法单位
在F中有元素 0 , 使得 \(\forall a \in F, a+0=a\)
- 存在乘法单位,且这个单位不同于加法单位0
在F中有不同于O的元素 1 ,使得 \(\forall a \in F, a * 1=a\)
- 存在加法逆元
\(\forall a \in F, \exists-a\) 使得 \(a+(-a)=0\)
- 非0元素存在乘法逆元
\(\forall a \in F, a \neq 0, \exists a^{-1}\) 使得 \(a * a^{-1}=1\)
\(Remark:\)
- 上面的八条公理看起来很乱,实际是为了定义这样的性质: \((F,+,*)\)中的\((F,+)\)是一个交换群(+运算有强对称性);\((F,*)\)也是一个交换群(*运算有强对称性); 并且*运算对+运算构成分配律(两种运算之间也有关系,且不对等)。反过来,如果(F,+)与(F,*)都是交换群,且*对+有分配律,那么他们合起来构成域(F,+,*)
- “元素0不同于元素1”的要求排除了平凡的只由一个元素组成的域
- 域是一个乘法可逆且乘法可交换的环。换句话说域在环的基础上增加了除法。实际上,域的另一个定义是: 域是交换性除环
环
环比域更宽泛,域是特殊的环。在上面域的讨论中,8条公理保证(F,+)和(F,*)都是交换群,且*对+有分配律。而环不要求(F,*)是交换群,仅要求为半群。环的严格定义如下:
集合 \(R\) 和定义于其上的二元运算 \(+\) 和·构成的三元组, \((R,+, \cdot)\) 构成一个环,若它们满足:
- \((R,+)\) 形成一个交换群, 其单位元称为零元, 记作 0 ,即:
- \((R,+)\) 是封闭的
- \((a+b)=(b+a)\)
- \((a+b)+c=a+(b+c)\)
- \(0+a=a+0=a\)
- \(\forall a \in R, \exists(-a)\) 满足 \(a+(-a)=(-a)+a=0,-a\) 称为 \(a\) 的加法逆元
- \((R, \cdot)\) 形成一个半群,即:
- \((R, \cdot)\) 是封闭的
- \((a \cdot b) \cdot c=a \cdot(b \cdot c)\)
- 乘法关于加法满足分配律,即(左分配和右分配):
- \(a \cdot(b+c)=(a \cdot b)+(a \cdot c)\)
- \((a+b) \cdot c=(a \cdot c)+(b \cdot c)\)
\(Remark:\)
- 一个环上的*运算如果满足*可逆且*可交换,那么构成一个域
- 如果*可交换,称为交换环
- 若环R是么环,且R\{0}对R上的乘法形成一个群,即: \(\forall a \in R \backslash\{0\}, \exists a^{-1} \in R \backslash\{0\}\), 使得 \(a^{-1} \cdot a=a \cdot a^{-1}=1\) 。则R称为除环。类似于把*运算理解成数域中的除法,显然除法也有对称性
向量空间
向量空间与域都有八个公理,而且他们有一些相似性,这两者也可以进行对比,引用下知乎上Yuhang Liu的观点
线性空间是一个加法群再配上一个域的数乘运算。它跟环最明显的区别是它上面没有乘法(数乘不是乘法),仅仅依靠线性空间的结构你不能把两个向量相乘。当然,线性空间上可以继续扩展结构,定义一种“有乘法的线性空间”,也就是 代数(是,代数 本身是一种代数结构,我不知道当时为什么人们要把它命名为代数。。),比如说 矩阵代数,它上面有加法,有数乘,还有自然的矩阵乘法。不严格地讲,代数就是一个既是线性空间又是环的东西(有人会把线性空间的条件放宽到模,但是很多文献里面讨论代数一般还是假定基底是一个域的)。
环就是一个既有加法也有乘法的东西,且加法和乘法之间满足一些相容性条件。域是一个乘法可逆且乘法可交换的环。
链接:https://www.zhihu.com/question/61294717/answer/186162348
向量空间定义如下:
给定域F,F上的向量空间V是一个集合,其上定义了两种二元运算:
- 向量加法 + : V + V → V,把V中的两个元素 u 和 v 映射到V中另一个元素,记作 u + v;
- 标量乘法 · : F × V → V,把F中的一个元素 a 和 V 中的一个元素u变为V中的另一个元素,记作 a ·u。
V中的元素称为向量,相对地,F中的元素称为标量。
向量+与数乘* 满足8条公理,此处不赘述。其中前四个公理说明装备了向量加法的V是交换群,余下的四个公理应用于标量乘法。需要注意的是向量之间的加法“+”和标量之间的加法“+”是不一样的,标量与向量之间的标量乘法·和两个标量之间的乘法(域F中自带的乘法)也是不一样的。
模
模(module)是对向量空间的推广,将标量需为域(向量空间)推广到任意环(模)。维基百科module部分原文如下:
A module over a ring is a generalization of the notion of vector space over a field, wherein the corresponding scalars are the elements of an arbitrary ring.
向量空间是F-模